
Конструкции, технические и эксплуатационные свойства транспортных средств
297
Учитывая эти допущения и особенности отражения эллиптическо-степенной модели
поглощающей способности шин, функциональная схема, эквивалентная передней или задней
подвеске двухосного автомобиля массового производства с учетом новой модели сглажи-
вающей способности шины, может быть представлена в виде, согласно рис. 1.
Как следует из рисунка, традиционная колебательная система, эквивалентная подвес-
ке автомобиля, с учетом модели переменного сглаживания шины дополнена новым звеном –
звеном сглаживания
J
, которое расположено между дорогой и шиной и осуществляет осред-
нение входного воздействия дороги на переменном интервале. Кроме того, в традиционной
системе организована обратная связь от всех звеньев колебательной системы к звену сглажи-
вания, отражающая функциональную зависимость параметра осреднения (длины пятна кон-
такта) от выходного параметра системы – нормального прогиба шины.
Математическое описание такой динамической системы кроме двух линейных диф-
ференциальных уравнений второго порядка, отражающих динамику двухмассовой колеба-
тельной системы, включает также интегральное уравнение с переменными пределами интег-
рирования, отражающее динамику звена сглаживания, и, в общем случае, нелинейное алгеб-
раическое уравнение обратной связи на параметр звена сглаживания. С учетом обозначений
рис. 1 система уравнений, описывающих движение масс колебательной системы и функцио-
нирование звена сглаживания, будет иметь следующий вид:
). (
)(
, )(
)(
1 )(
,0 )
( 2 )
(
)
( 2 )
(
,0 )
( 2 )
(
2/)(
2/)(
z
lal
lal
cг
p
п
cг
z
cг
шэ
p
п
hF la
dl lq
la
l q
zC z
q С q
m
zС z
zM
(1)
С точки зрения теории автоматического регулирования рассматриваемая колебатель-
ная система (рис. 1) является замкнутой системой автоматического регулирования (САР) с
обратной связью на параметр, состоящая из четырех звеньев: звена переменного сглажива-
ния, звена смены аргумента, колебательного звена второго порядка и звена обратной связи.
Обратная связь организована с выхода системы по нормальному прогибу шины на параметр
осреднения звена сглаживания. На вход системы подается случайный стационарный сигнал с
нормальным законом распределения, пропорциональный смещению ординат микропрофиля
дороги.
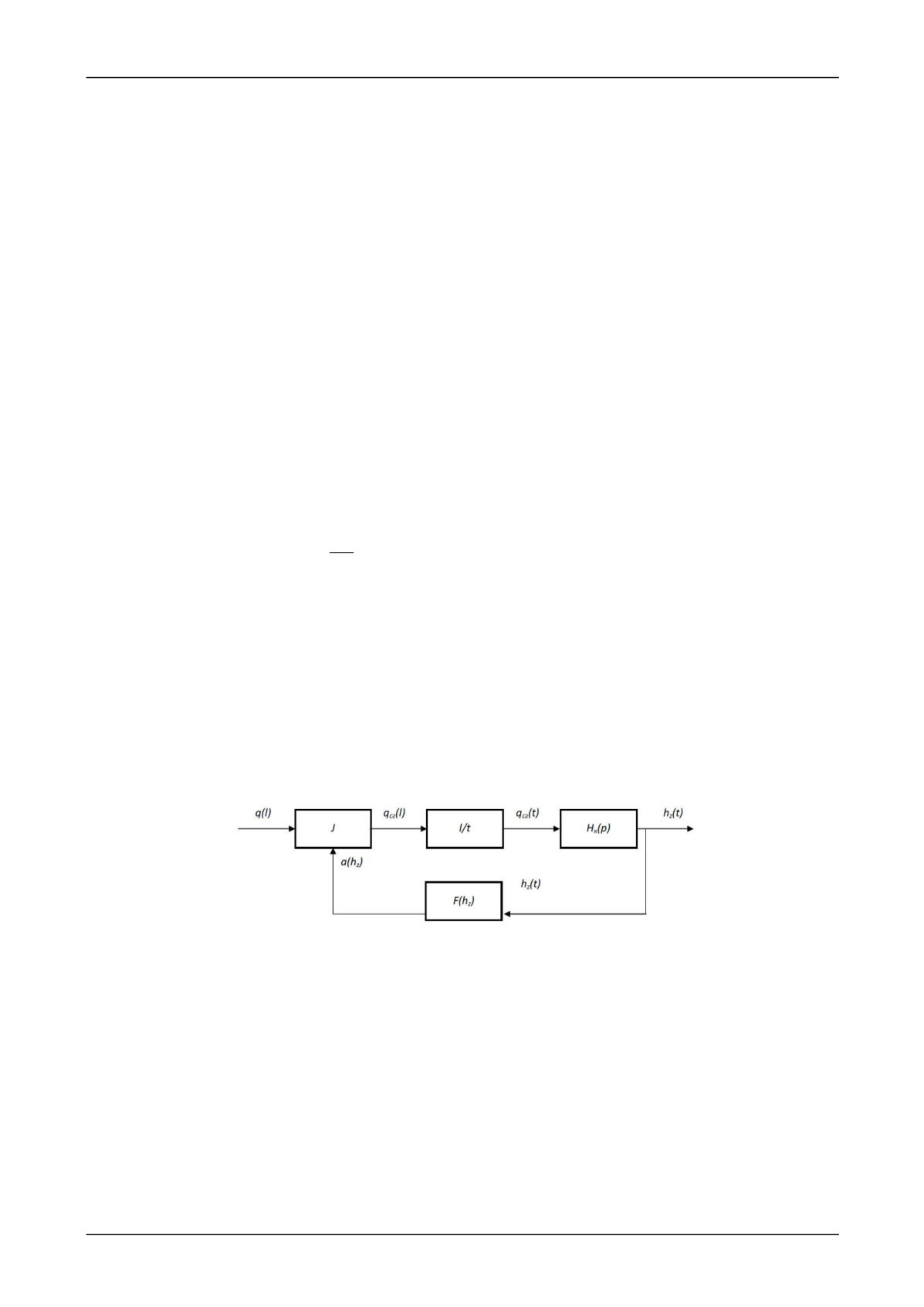
Структурная схема такой системы автоматического регулирования изображена на рис. 2.
Рис. 2. Структурная схема САР, эквивалентная колебательной системе передней
(задней) подвеске автомобиля, с учетом модели переменного сглаживания шины:
J
– звено переменного сглаживания; l/
t
– звено смены аргумента;
H
к
(
p
) – колебательное звено второго порядка;
F
(
h
z
) – звено обратной связи;
q
(
l
),
q
сг
(
l
),
q
сг
(
t
) – функции исходного и сглаженного микропрофиля;
h
z
(
t
) – функция деформации шины;
a
(
h
z
) – функция параметра сглаживания
В случае линейных стационарных систем, на вход которых подается воздействие в
виде случайной стационарной функции с известными статистическими характеристиками
(корреляционной функцией или спектральной плотностью), задача анализа успешно решает-
ся, поскольку удается получить аналитические выражения передаточных функций и частот-
ных характеристик системы, в том числе и звена сглаживания, как и статистических характе-
ристик сигналов на выходе.
Для нелинейных систем автоматического регулирования аналитические методы ста-
тистической динамики линейных САР не пригодны. Методы нелинейной статистической ди-
















