
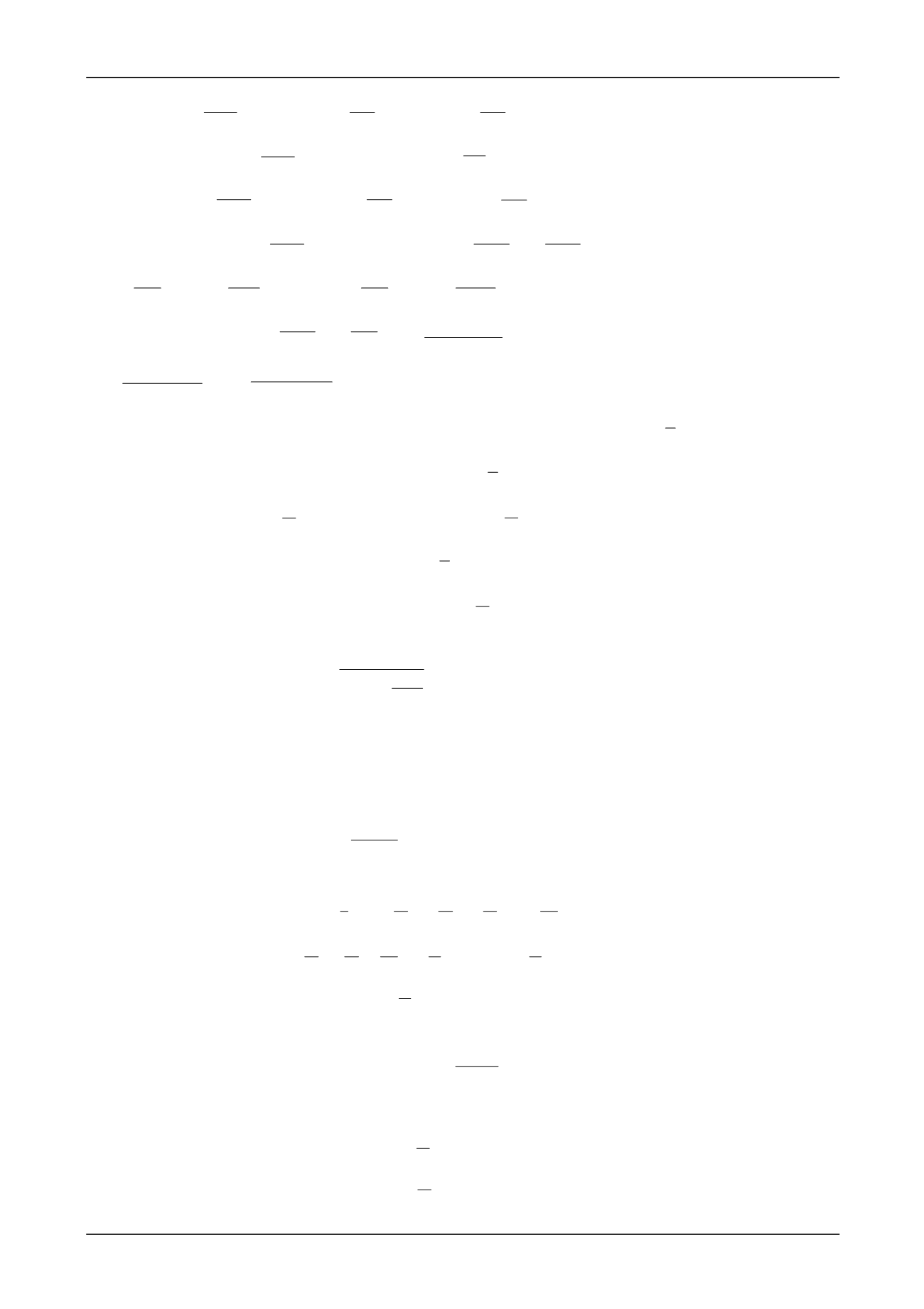
Материаловедение, динамика и прочность машин и механизмов
273
1,1
8,8
1,8
3
4
;
y
y
EI
k k
k
A
l
5,5
12,12
1 ;
y
y
EI
k k
A
l
5,12
1 ;
y
y
EI
k
A
l
1,5
1,12
5,8
8,12
2
2
;
y
y
EI
k k
k
k
A
l
3,3 10,10
3,10
;
EA
k k
k
l
2,2
9,9
2,9
3
4
;
x
x
EI
k k
k
A
l
4,4 11,11
1 ;
x
x
EI
k k
A
l
4,11
2
1 ;
x
x
EI
k
A
l
4,9
9,11
2,4
2,11
2
2 ;
x
x
EI
k k
k
k
A
l
ω
6,6
13,13
6,13
ω 3
4
6 ;
5
k
EI
GI
k k
k
A
l
l
ω
7,14
1
;
30
k
y
EI
lGI
k
A
l
ω
7,7
14,14
2
1
;
5
k
y
EI
lGI
k k
A
l
ω
7,13 13,14
6,7
6,14
ω 2
2
;
10
k
EI
GI
k k
k
k
A
l
2
1,2
;
xy
x y
x
y
K E I I
k
GA K K l
(18)
2
ω
ω
1,6
ω
;
y
y
y
K E I I
k
GA K K l
2
ω
ω
2,6
ω
;
x
x
x
K E I I
k
GA K K l
8,9
1,2
1,9
2,8
;
k k
k
k
8,13 1,6
1,13
8,6
;
k k
k
k
1,4
1,11
9,12
2,12
2,5
4,8
5,9
8,11
1,2
;
2
l
k k k
k
k
k k k
k
1,7
1,14 12,13
6,12
5,6
5,13
8,14
7,8
1,6
;
2
l
k k k
k
k k
k
k
k
2
4,5
5,11
4,12
11,12
1,2
;
4
l
k k k k
k
2
5,7
5,14
7,12
12,14
1,6
;
4
l
k k k k
k
2,7
2,14
9,14
6,11
4,6
7,9
4,13
2,6
;
2
l
k k
k k k
k
k
k
9,13
2,6
2,13
9,6
;
k k
k
k
2
4,7
4,14
11,14
7,11
2,6
,
4
l
k k k
k k
где, согласно [5],
2
3
,
, , ω
1 12
i
i
ii
A
i x y
EI K
l GA
.
(19)
Теперь укажем, что при расчёте пространственных конструкций, составленных из
тонкостенных стержней, на динамическое воздействие по МКЭ необходимо знать не только
матрицу жёсткости (4), но и матрицу масс каждого стержня [11].
Аналогично (17), инерционные коэффициенты матрицы масс КЭ
jk
вычисляются по
формуле:
2
,
,
1, 2, ..., 14,
jk
j
k
T
m
j k
q q
(20)
в которой
Т
– кинетическая энергия деформации КЭ
jk
2
2
2
2
2
0
2
2
2
ω
ωω
ω
1
ξ
η
ζ
ρ
2
ξ
η
2
ξ φ
η φ
1
φ
,
l
y
x
y
y
x
x
T
A
r
t
t
t
t
A a
a
I
I
t
t
t
t
t
I
K
dz
t
(21)
в которой
2
2
2
x
y
x
y
I I
r a a
A
.
(22)
В формулах (21) и (22) ξ, ζ, η – компоненты перемещения центра изгиба (11) стержня
с координатами [11] (см. рис. 2):
ω
ω
1 ω
,
1 ω
,
x
x
b
x
x A
y
y
b
y
y A
a b
ydA K
I
a b
xdA K
I
(23)
















