
Материаловедение, динамика и прочность машин и механизмов
271
точке концевого сечения
j
(
k
) тонкостенного КЭ
jk
с учётом депланации
( )
j k
B
определяется по
формуле [5]:
( )
( )
( )
( )
( )
j k
j k
j k
j k
y
j k
x
z
c
x
y
M M N
B
y
x
A I
I
I
,
(7)
где
x
,
y
– линейные координаты заданной точки сечения;
с
и
I
– секториальная ко-
ордината и секториальный момент инерции сечения. Касательные напряжения в произволь-
ной точке концевого сечения
j
(
k
) тонкостенного КЭ
jk
открытого профиля определяется по
формуле [5]:
( )
( )
( )
( )
( )
( )
( )
0
п
с
2
j k j k
j k j k
j k
j k
x
y
y
x
j k
y
x
c
cd
Q S Q S M S M
I t
I t
I t
I t
;
(8)
закрытого профиля коробчатого (замкнутого) сечения:
( )
( )
( )
( )
( )
( )
( )
с
2
2
j k j k
j k j k
j k
j k
x
y
y
x
j k
z
y n
x
c
с
Q S Q S M S M
I t
I t
I t
A t
,
(9)
где
0
z
M M M
– суммарный крутящий момент;
o
d
M G I
- крутящий момент;
M
– изгибно-крутящий момент;
– производная от угла закручивания,
А
– удвоенная
площадь контура коробчатого (замкнутого) сечения;
( , )
x y
S
– статические и секториально-
статический моменты отсечённой площади в рассматриваемом сечении;
( )
c n
t
,
( )
c n
I
– толщина
стенки (полки) и её осевой момент инерции.
Эквивалентные напряжения в любой точке сечений с учётом (7) – (9) определяются по
третьей теории прочности:
( )
( )
( ) 2
э
4(
)
j k
j k
j k
R
.
(10)
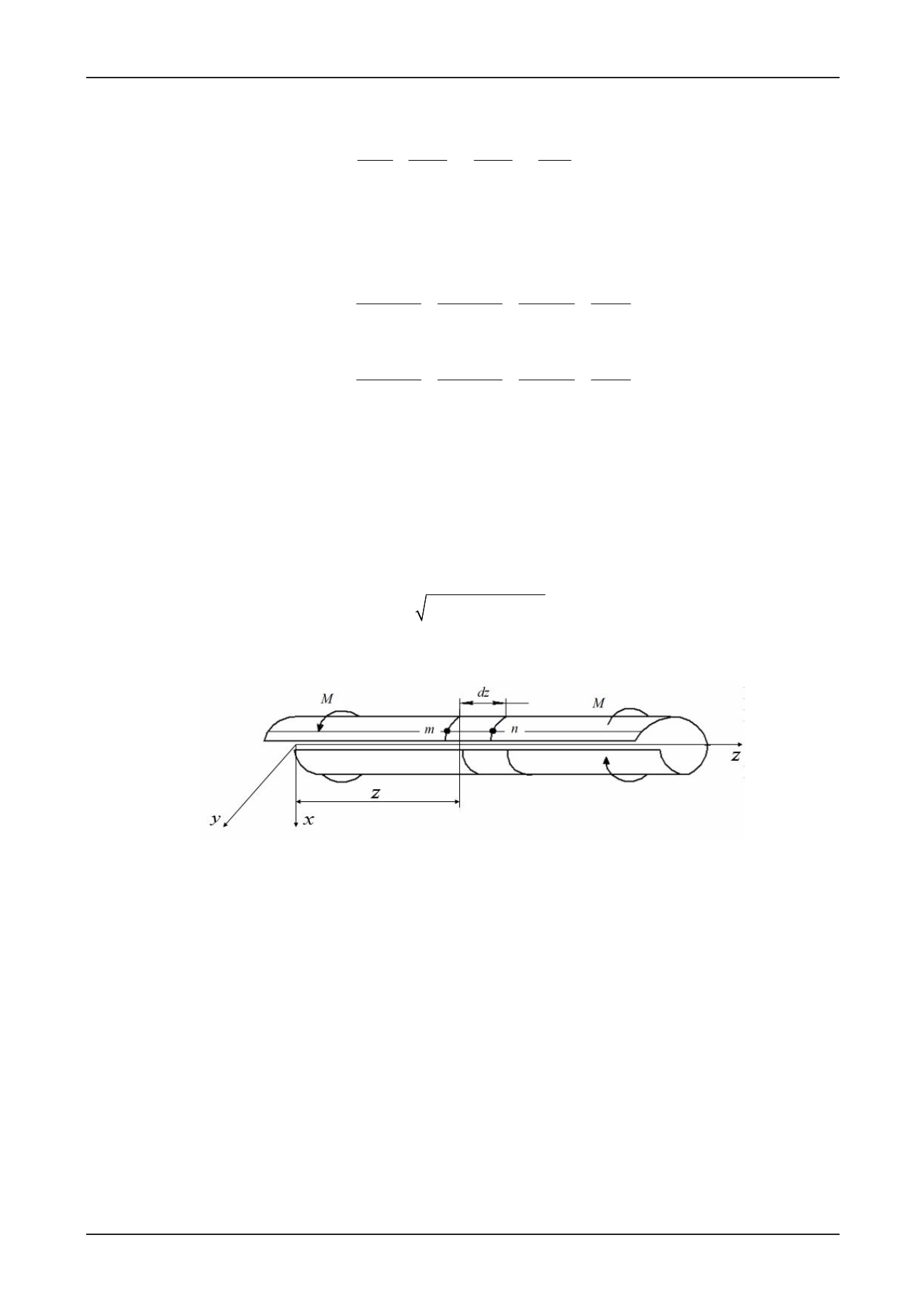
Исходя из предпосылок, представленных в [9-11], рассмотрим наиболее характерные
стороны теории тонкостенных стержней открытого профиля (рис. 1).
Рис. 1. Равновесие выделенного элемента тонкостенного стержня открытого профиля
Особенностью и новизной полученных решений является учёт влияния сдвигов сре-
динной поверхности тонкостенных стержней открытого профиля на их напряжённо-
деформированное состояние [5].
Значения элементов искомой матрицы жёсткости (3) при прочностном расчёте зави-
сит от жёсткостных параметров КЭ и принятого закона изменения компонентов межузловых
перемещений, в качестве которых примем аппроксимирующие функции Эрмита [9]:
( )
( ),
1,5,8,12,
( )
( ),
2,4,9,11,
( )
( ),
3,10,
( )
( ),
6,7,13,14,
s s
s s
s s
s s
z
q z s
z
q z s
z
q z s
z
q z s
(11)
в которых
q
s
– узловое перемещение:
s
= 1, 2, …, 14, как степени свободы (
n
= 14) уз-
ла;
s
(
z
) – аппроксимирующие функции Эрмита тонкостенных стержней открытого и замк-
нутого профилей с двумя осями симметрии жёстко защемлённого по концам с учётом сдвига
срединной поверхности, имеющие вид [12]:
















