"Механики XXI веку" №16 2017

272 / 397

Механики XXI веку. №16 2017 г.
272
2 3
2, 1, 6,ω
2 3
3
4, 5, 7,ω
2 3
9, 8, 13,ω
11,
1 1
ψ ( ) ψ ( ) ψ ( ) 1 2 ;
4 6
1
ψ ( ) ψ ( ) ψ ( ) 1 1 ;
2 4 2 12
1 1
ψ ( ) ψ ( ) ψ ( ) ;
4 6
ψ ( )
ii i
x y
i i i
ii i
x y
i i i
ii i
x y
i i i
x
K EJ
z z z z z z
K l GA K K l
K EJ l z
z z z z z
K GA K l K
K EJ
z z z z z z
GA K l K K l
z
         
   
           
   
   
        
   
2 3
12, 14,ω
3, 10,
1 1
ψ ( ) ψ ( ) ;
2 8 2 12
ψ 1 ; ψ ,
ii i
y
i i i
z z
K EJ l
z z z z z
GA K K l K
z z l z z l
 
          
 
  
(12)
в которых
2
,( , , ω)
12
i
i ii
EJ l
K K i x y
GA
   . (13)
Следуя (11) и (12), учтём влияние деформации сдвига, включив в выражение для по-
тенциальной энергии деформации тонкостенного стержня открытого профиля V ту её часть,
которая вызвана работой касательных напряжений (8) [9 - 11]:
           
      

2 2 2 2 2
ω
0
2 2 2
ωω ω
0
ω ω ω ω
1 ζ ξ η
2
1 ξ η
2
2 η ξ 2 ξ 2 η ,
l
y x d
l
yy y xx x
xy x y y y x x
V EA EI EI EI GI dz
K EI K EI K EI
GA
K EI EI K EI EI K EI EI dz
            
       
          


(14)
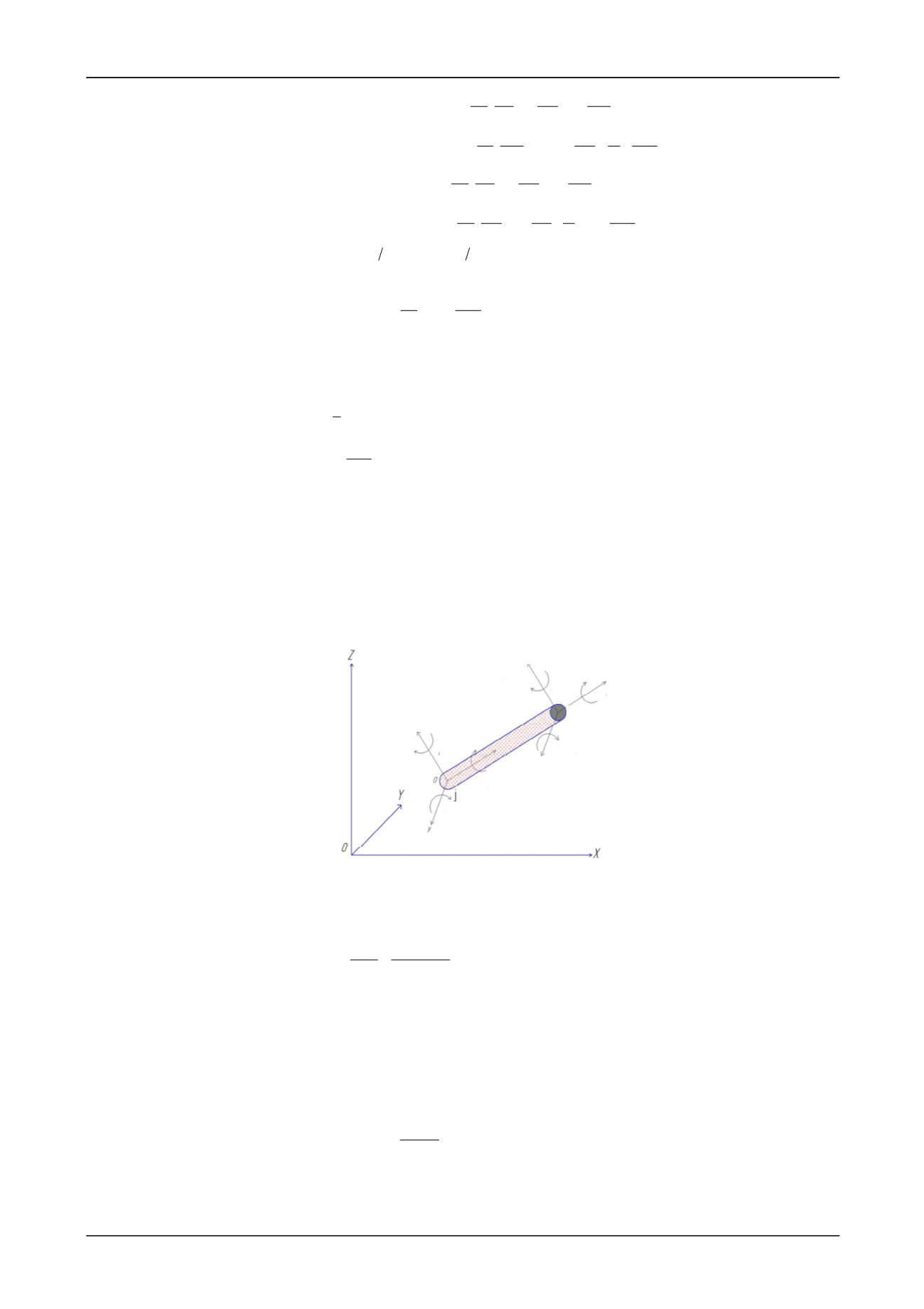
в которой ξ, η, ζ – перемещения точек линии центров изгиба стержня в направлении
осей МСК x, y и z (рис. 2), а также известные зависимости:
ω ω
ω ω
ς ; η ;
ξ ; η ;
ξ ; .
;
x x
y y x y
y x
EA N EI M
EI M EI Q
EI Q EI M
EI B
    
    
     
   
(15)
xK
 xH
yH
yK
ΘzK
ΘzH
ξH
ξK ζK
ζH
ηH
ηK
K
x
x
z
y
Рис. 1. Правило знаков для узловых перемещений (степеней свободы)
тонкостенных стержней в местной системе координат (МСК)
Кроме (15), в (14) коэффициенты Kij определяются по формуле:
( ) ( )
2 ; , , , ω
δ
i s j s
ij
i j A
S S A K dA i j x y
I I
   . (16)
Для симметричных профилей, если сечение тонкостенного стержня симметрично от-
носительно оси х, в (11) Kxy = Ky = 0. Если осью симметрии является ось у, то Kxy = Kх = 0.
Если же сечение симметрично относительно обеих главных осей, то Kxy = Kхω= Kyω = 0.
После чего любой ненулевой элемент матрицы жёсткости тонкостенного стрежня от-
крытого профиля (3) в МСК при пространственном деформировании с учётом сдвига сре-
динной поверхности определяется по формуле:
2
, , 1, 2, ..., 14,
jk
j k
V Kj k
q q

 
 
(17)
в которой V – потенциальная энергия деформации (14), а q j(k) – обобщённые переме-
щения (степени свободы) узлов КЭ jk: