
Механики XXI веку. №16 2017 г.
266
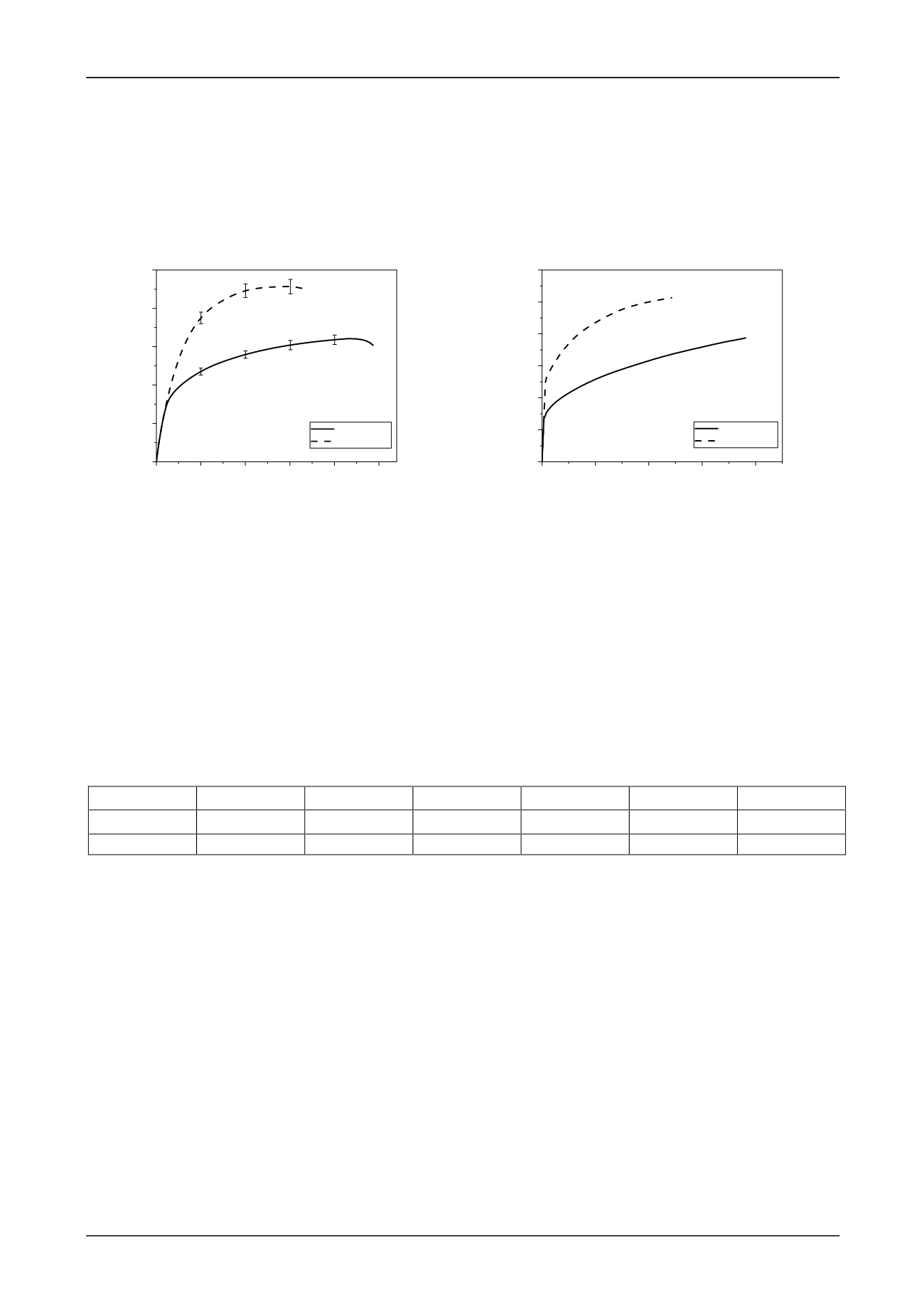
На рис. 3а представлены экспериментальные зависимости напряжений от деформаций
в условных координатах при одноосном растяжении двух партий плоских образцов из ис-
ходного сплава 1560 и после его обработки РКУП. В каждой партии испытано по 5 образцов.
Значения интервалов достоверности удовлетворяют погрешности эксперимента до 5 %. По-
сле четырехпроходной обработки у исследуемого сплава отмечено увеличение условного
предела текучести σ
0,2
на 80 %, временного сопротивления σ
в
на 44 % и уменьшение пре-
дельной деформации до разрушения ε
max
в условиях растяжения на 30 %.
0.00 0.05 0.10 0.15 0.20 0.25
0
100
200
300
400
500
исходный
после РКУП
ing
(MPa)
ing
0.00 0.05 0.10 0.15 0.20
0
100
200
300
400
500
600
true
(MPa)
true
исходный
после РКУП
а)
б)
Рис. 3. Зависимости напряжений от деформаций в образцах из сплава 1560 при одноосном
растяжении
а
– в условных координатах;
б
– в истинных координатах
Эффекты увеличения микротвердости, условного предела текучести и временного со-
противления при растяжении с одновременным уменьшением предельных деформаций до
разрушения после различных режимов и схем обработки ИПД являются характерной осо-
бенностью алюминий-магниевых сплавов [1,7 - 9].
Продольная скорость звука в сплаве в состоянии поставки и после обработки колеб-
лется в пределах 0,04 % и составляет 5440±2 м/с, что соответствует модулю Юнга
E
равному
78±0,3 ГПа. Сводные данные по физико-механическим свойствам исследуемого сплава пред-
ставлены в таблице 1.
Таблица 1
Физико-механические свойства сплава 1560 в исходном и обработанном состояниях
Образец
d
g
(мкм)
HV (МПа)
σ
0,2
(МПа)
σ
в
(МПа)
ε
max
E
(ГПа)
Исходный
50
1000
150
320
0,24
78
РКУП
3
1550
270
460
0,17
78
При оценке возможных областей применения материала и способов его обработки в
изделия методами резания, фрезерования, штамповки часто обращаются к помощи компью-
терного моделирования. Для этого необходимо подбирать адекватные определяющие соот-
ношения, способные описывать эффекты пластического течения и упрочнения. На практике
при обработке экспериментальных данных и использовании их в расчетных модулях попу-
лярных инженерных приложений довольно часто используется условие проведения степен-
ной аппроксимации, когда аппроксимирующая функция имеет две общие точки с экспери-
ментальной кривой. Обычно эти точки соответствуют началу пластического течения (истин-
ный предел текучести
S
0,2
) и моменту образования шейки (истинное напряжение
S
в
при де-
формации ε
p
). При этом необходимо представить экспериментальные зависимости напряже-
ний от деформаций в истинных координатах, см. рис. 3б. Участок упругого деформирования
на графике соответствует модулю упругости
Е
, полученному при измерении скорости про-
хождения продольной упругой волны. В этом случае упруго-пластическое поведение спла-
вов можно аппроксимировать функцией Холомона [10]:
















