
Материаловедение, динамика и прочность машин и механизмов
281
Описание модели
. Для изучения возможности подтапливания рабочего органа загла-
живающей машины и возникающих, при этом крутильных автоколебаний, будем исходить из
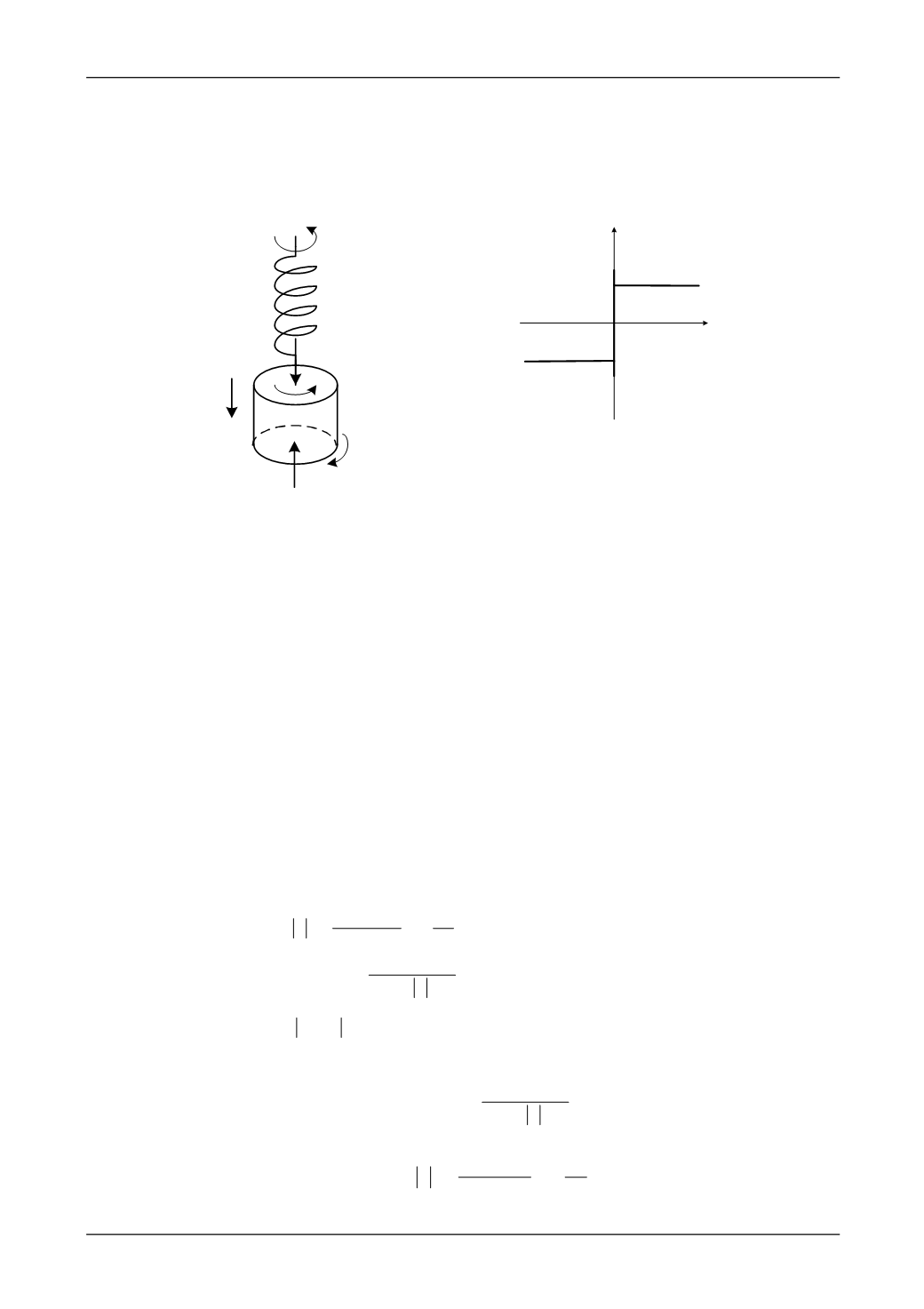
простейшей одномассовой модели (рис.1), которая принципиально никак не отличается от
ранее введенной модели для бурильной колонны [6], добавив при этом вибрационную силу
.
sin
t
H
t
b
C
M M
c
C
F
V
t
Hmg
sin
0
1
1
0
Рис. 1. Динамическая модель заглаживаю-
щей машины
Рис. 2. Закон Кулона
Здесь предполагается, что вал электродвигателя имеет постоянную угловую скорость
, а через упругое передаточное звено – пружину, вращение передается к заглаживающему
диску, угол закручивания которого
,
и на который со стороны забоя действуют момент
c
M
и сила
c
F
сопротивления (
Im
,
соответственно масса заглаживающей машины и осевой мо-
мент инерции заглаживающего диска радиуса
R
); V – текущая скорость подтапливания дис-
ка. Упругий момент со стороны упругого передаточного звена, введем согласно закону Гука:
),
(
t
c M
где
t
текущее время,
c
жесткость пружины кручения, определяющая упру-
гие свойства передаточного звена; момент сил вязкого сопротивления
b
M
примем равным:
,
2
a M
b
где
a
- коэффициент вязкого сопротивления; точкой обозначена производная по
времени
t
.
Постановка и решение задачи.
Задача рассматривается в простейшей постановке,
когда диск заглаживает бетонную смесь в одном месте заданное время, то есть без учета
движения диска в горизонтальном направлении вдоль обрабатываемой поверхности. Кроме
того, предполагается, что диск может кратковременно заклинивать в поступательном движе-
нии при погружении и во вращательном. Согласно теории погружения вращающегося твер-
дого тела в грунт, изложенной, например, в работах [6, 7], получим:
.0
,
;0
,
sin 1
;0
,
;0
,
sin 1
,0
;0
,
sin 1
;
1
sin 1
,0
10
0
2
11
1
1
1
x при
sign
bR x
x
mg n
x при
sign t
h mg
t
c
sign a I
x при mgn
x при t
h mg
t
c при
x при
bR x
x gn t
h g x
bR t
h
n
при
x
(1)
Остановку погружения диска следует ожидать тогда, когда одновременно будет:
.
1
sin 1
0
0
1
1
bR t
h
n
и x
и x
д
(2)
















