
Механики XXI веку. №16 2017 г.
228
при этом
s
1 .
Таким образом, в данном случае получены выражения, тождественные выражениям (12).
Для фрактальной модели шероховатости относительная высота отдельной неровности
ω находися в пределах 0,15…0,25. Если принять, что высота отдельной неровности ω являет-
ся постоянной величиной, то распределение выступов неровностей для такой фрактально-
дискретной модели шероховатости определяется выражениями [16, 17]:
n
k
n
k u
u
0
3
,
(15)
,
11
1
11
1
,
2
1
0
1
2
3
k u
k u
k u
k u
u
n
k
n
(16)
где
u
n
int
,
1
1
1 1
1
,
m
k
k k
.
(17)
Решение уравнения (17) дает несколько значений ω, из них выбирают то, при кото-
ром распределение вершин неровностей максимально соответствует реальной поверхности.
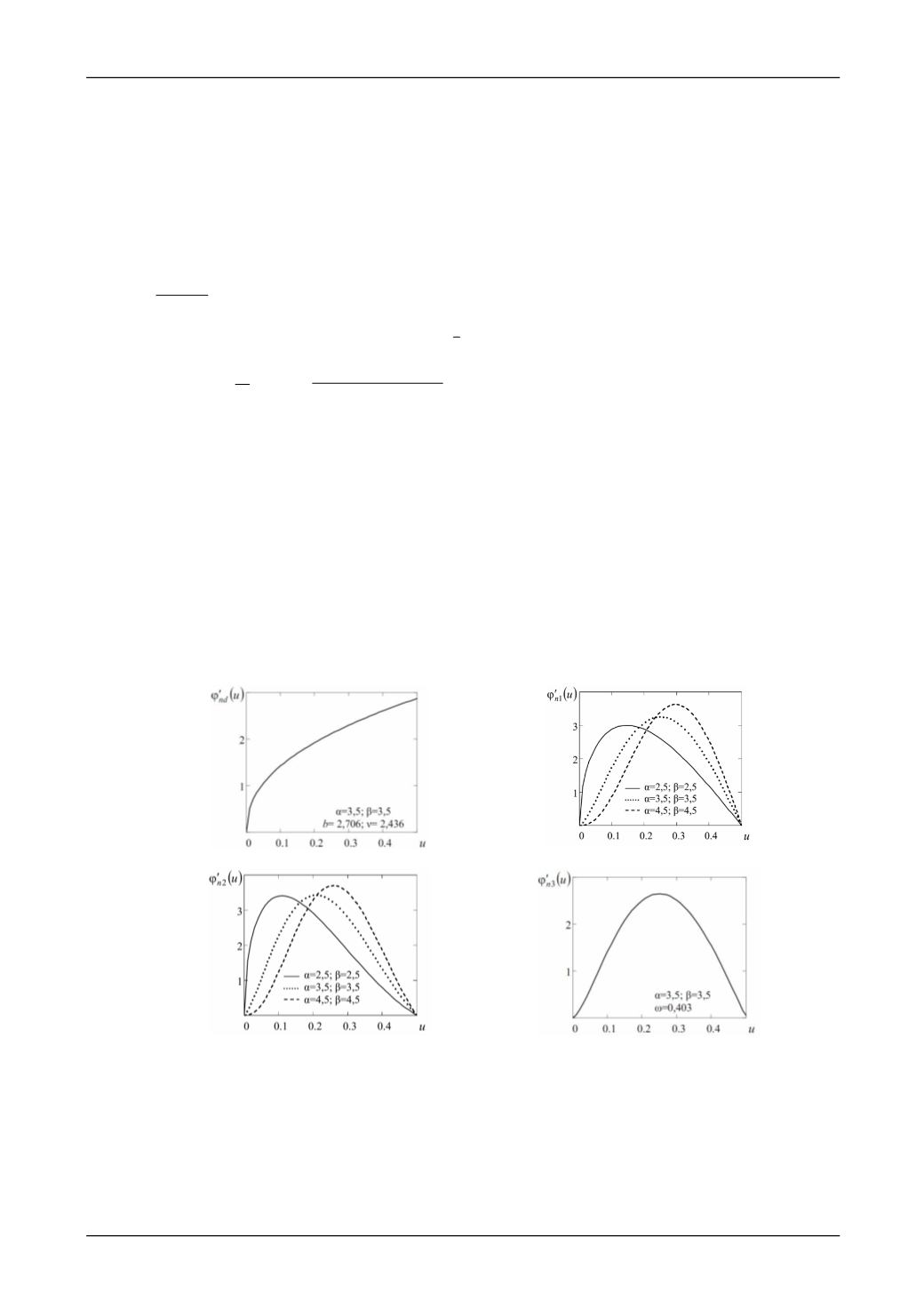
Вид функций плотности распределения высот неровностей, описываемых выраже-
ниями (4), (12), (13) и (16) для разных значений параметров α и β, показан на рис. 2
а
– 2
г
соответственно.
Как следует из рисунка 2, число неровностей, находящихся выше уровня
u
= 0,25…0,30,
для кривых на рис.2
б, в, г
примерно в 1,5 раза больше, чем для кривой на рис. 2
а
, что значи-
тельно сказывается при определении характеристик контакта шероховатых поверхностей. Мо-
дель шероховатой поверхности, соответствующая рис. 2
а
, следует использовать для
u
<(0,1…0,15), т.е. при контактировании неровностей соответствующих верхней части опорной
кривой.
а)
б)
в)
г)
Рис. 2. Функции плотности распределения выступов неровностей
u
ni
Совпадение значений, определенных с помощью выражений (12) и (14), для функций
n
и
n
свидетельствует о качественном описании шероховатости с помощью упрощенной
модели. Причем при определении контактных характеристик будет использоваться одномер-
ная функция распределения неровностей, что значительно упростит расчеты.
4. Параметры эквивалентной шероховатой поверхности
















