
Механики XXI веку. №16 2017 г.
226
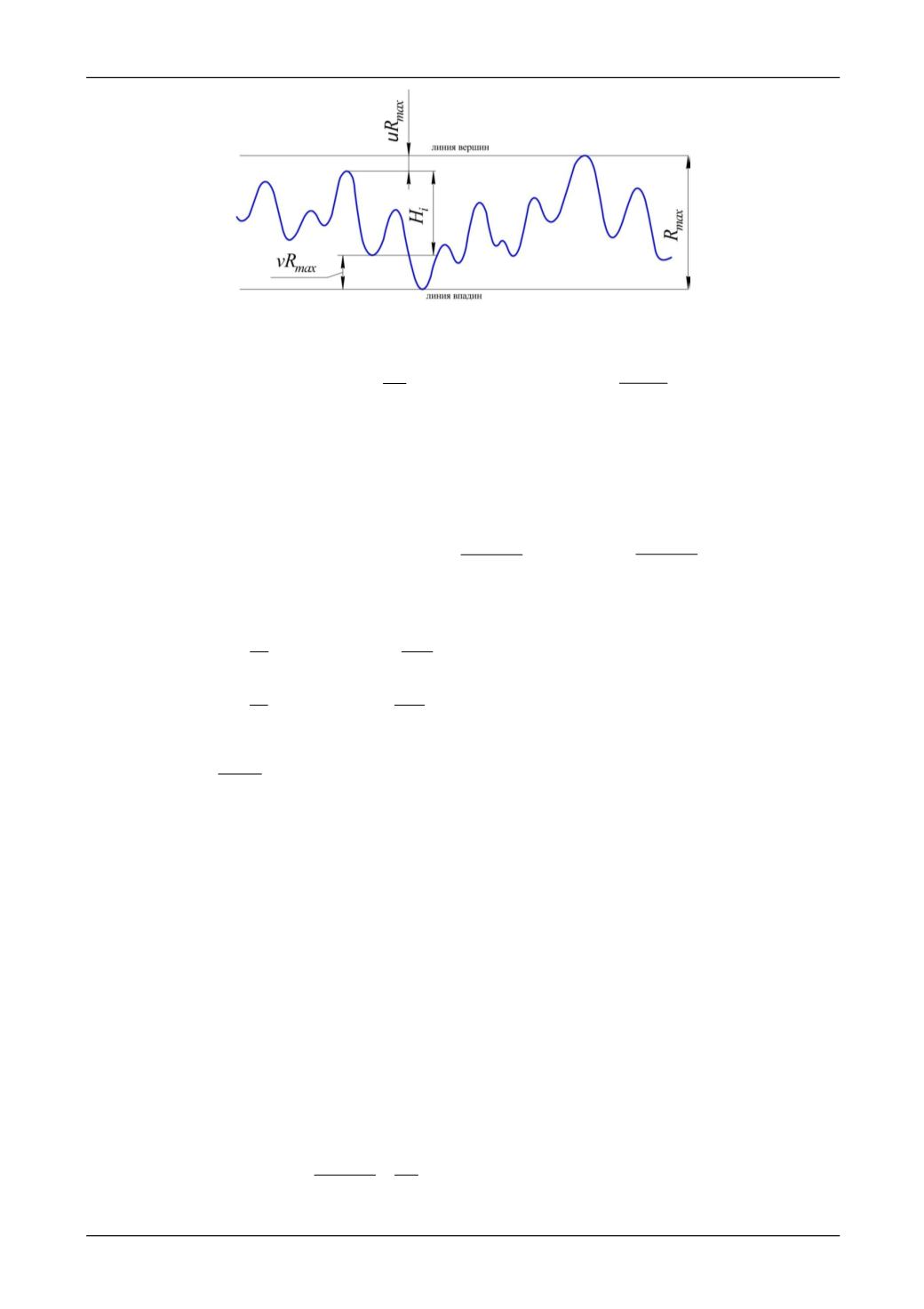
Рис. 1. Схема шероховатой поверхности
Для описания всей шероховатой поверхности при известных функциях необходимо
знать одну из двух функций:
u
c
u
u
A
A
1
или
c
n
n
vun vu
,
,
,
где
; /
c v
v
AA n
;1
A
u
,
A
v
– площадь сечения материала и свободного полупро-
странства на относительных уровнях
и
;
n
(
u,v
) – число неровностей, вершины которых
расположены выше уровня
u
, а впадины – ниже уровня
v
;
n
c
– общее число неровностей. То-
гда задача сводится к определению
n
(
u,v
).
Допустим, что функция
u
(
) монотонная и дважды дифференцируемая для
[0, 1] и
описывается выражением (2):
,
,
,
,
B
B
I
u
,
,
B
B
.
Считая, что функции
ui
(
i
),
c
(
),
n
(
u, v
) монотонны и непрерывны, получим сле-
дующие выражения:
;
,
,
1
1,
min
,
min
,
min
0
,
min
0
dvvu
dvvu
u
du
C
n
u
c
n
c
ui
a
u
s
s
s
s
(5)
;
,
,
1
1,
min
,
min
,
min
0
,
min
0
duvu
duvu
v
dv
C
n
v
c
n
c
vi
a
v
s
s
s
s
(6)
где
s
s
s
s
u
n
c
u
n
c
c
cm
a
duvu
dv
dvvu
du
A
A
C
0
1,
min
0
0
1,
min
0
max
;
,
,
s
,
s
– уровни на-
сыщения вершин и впадин.
Решение уравнений (5), (6) относительно
n
(
u,v
) без наличия каких-либо гипотез, ка-
сающихся вида функции
n
(
u,v
) и соотношения параметров
s
и
s
, даже при известных
функциях
ui
(
i
) и
v
i
(
i
) представляет собой некорректную задачу. Поэтому сделаны сле-
дующие допущения:
1. Функцию
vu
n
,
можно представить в виде:
fv fu f
vu
v
u
n
,
,
(7)
где функция
1
1
1
1
1
f
определяет спектр неровностей и служит мерой
взаимозависимости функций распределения вершин и впадин.
2.
1
s
s
.
3. Вершины и впадины имеют одинаковую форму и их описывают параболоидом вто-
рого порядка. Тогда:
;
i
i
ui
.
i
i
vi
4.
.1,0
;
c
С учетом допущений из уравнений (5) и (6) получим систему парных уравнений
Фрейгольма первого рода
;
1
1
0
1
1
2
2
1
1
s
dvv f
v
v
f
C d
d
v
u
a
u
u
(8)
















