
Материаловедение, динамика и прочность машин и механизмов
259
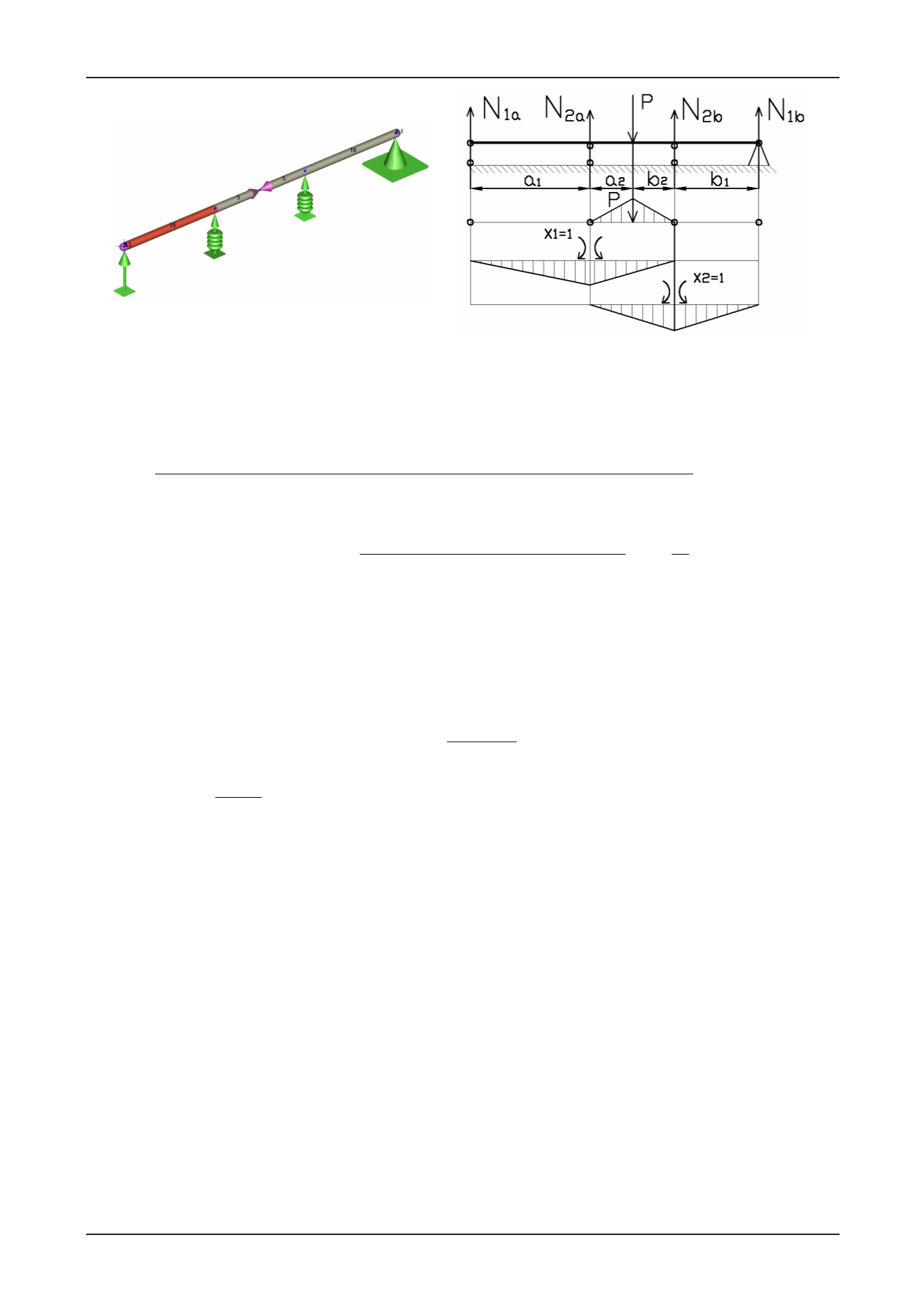
Рис.3. Участок технологического трубопровода
(в программе СТАРТ-PROF 4.61)
Рис.4. Расчетная модель симметричной
конструкции – участка технологических
трубопроводов, работающей на изгиб (метод сил)
Согласно (1), неизвестные реакции в опорах трубопроводов
N
iа
,
N
ib
,
i
= 1, 2 можно оп-
ределить по формулам:
) 5,0 (
1
2
2
2 1
2
2
2
2 1
2
2 1
2
2
2
2 1
2
2 1
2
2 1
2
2 2
2
2 1
2
2 1
2
2 2
2
2
2 1
2
2 1
2
2
2
a
aq
a abac b bbac a a b bac a a b bbc
c a a b bb
Р N
b
a
b
a
a
a
(2)
2
1
2 1 2
1
2
2 1 2
2 1
1 2
1
aq
b b a a
a b bN b bP bN
N
a
b
a
.
Формулы для определения реакций
N
ib
,
i
= 1, 2, очевидно, можно записать, заменив
индекс/переменную
a
на
b
. Последним слагаемым в выражениях (при
q
) учтено влияние рав-
номерно-распределенной нагрузки
q
(вес среды и материала труб с изоляцией).
Жесткость
c
iа
,
c
ib
,
i
= 1, 2 (обратную величину податливости) при изгибе следует опре-
делять как составную – состоящую из жесткости как самой трубы, так и опорных конструк-
ций (связей):
)
h
ia
tr
ia
h
ia
tr
ia
ia
c c
c c
c
,
i
=1,2;
где
3
i
tr
x
tr
ia
a
JE c
– жесткость участка трубы
a
i
.
Здесь
tr
x
J
– осевой момент инерции се-
чения трубы;
h
ia
c
– жесткость опорной конструкции.
Проверка приведенных формул производилась сравнением с точными решениями,
полученными методом сил и МКЭ в программной среде СТАРТ-PROF 4.61. Получено, что
данное решение совпадает с точным, в случае
c
iа
=
c
ib
=1,
i
= 1, 2 (жесткость опор не учитыва-
ется). Учет жесткости опор приводит к погрешности 10 - 20%.
Практическая ценность, полученных на оснований вышеозвученных формул, возрас-
тает из-за возможности учитывать незначительную асимметрию с удовлетворительной по-
грешностью [3].
В результате исследования получены следующие выводы:
а) решение, полученное из предположения об обратной пропорциональности реакций
квадрату расстояния до точки приложения силы, в статически неопределимых, симметрич-
ных стержневых системах, при растяжении/сжатии и изгибе, совпадает с точным и может
широко использоваться на практике;
б) решение, полученное из предположения о пропорциональности реакций удельной
жесткости связей, в статически неопределимых симметричных стержневых системах, при
растяжении/сжатии совпадает с точным и может широко использоваться на практике;
















