
Материаловедение, динамика и прочность машин и механизмов
213
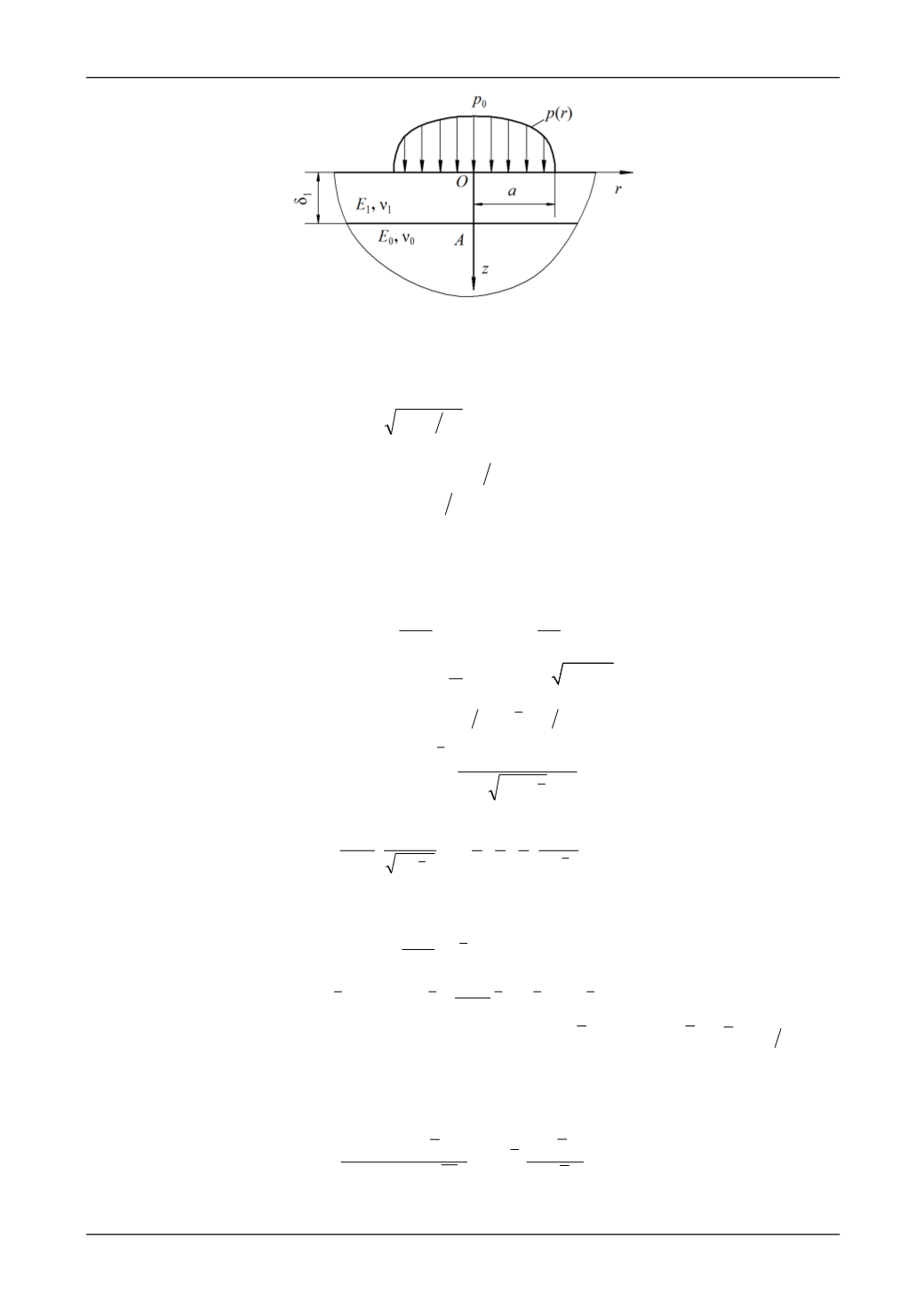
Рис. 1. Схема нагружения слоистого тела
Авторами [13, 14] на основании жесткостной модели определена упругая характеристика
полупространства с однослойным покрытием для любых значений
1
при нагружении слоисто-
го полупространства (рис. 1) нормальными напряжениями в круговой области:
2 2
0
1
)(
a r
p rp
,
a r
0
(1)
В дальнейших работах [15, 16] рассмотрена нагрузка более общего вида:
2 2
0
1 )(
a r p rp
,
(2)
где
5,0 0
,
1
0
m
p p
,
2
a P p
m
– среднее давление.
Следуя классическому подходу, основанному на применении потенциальных функций
Буссинеску [17], для перемещения любой точки по оси симметрии внутрь однородного
полупространства для случая его нагружения распределенной нагрузкой (1) определяются
выражениями:
1
d
2 1
2
d
z
u
z
E
z
,
(3)
1 d d
s
p r r r
R
,
2
2
R r z
.
С учетом выражения (1) и того, что
ar
и
az z
,
2
0
1
0
2
5.02
0
1
4
z
dd
ap
.
(4)
После интегрирования имеем:
2
1 2 2
0
1
1 ;
2
5 ;
2
3 ,
2
1
1
1
1
z
F
z
ap
,
(5)
где
xcbaF
; ; ,
1 2
– гипергеометрическая функция Гаусса.
Подставляя выражение (5) в (3) получим:
,
*
zK
E
ap u
m
z
,
(6)
z
z z
z
zK
arcctg
1
1
arcctg
,
(7)
Упростим обозначения, приняв
0
, ,0
i
i
i
K
K
,
1
1
,, ,
i
i
i
K
K
,
a
1
1
.
Для эффективного модуля упругости и коэффициента Пуассона топокомпозита в ра-
ботах [12, 13] получено:
1
*
1
*
01
FE E
;
(8)
1
1 01
1 0
1
1 01
01
2
1 1
1
1
1
0
0 0
e
I
K
K K
K K
K K K F
;
(9)
















