
Материаловедение, динамика и прочность машин и механизмов
239
1
1
**
0
2
max
0
0
.
8
3,2 exp
l
u
з
i
n r i
cQ
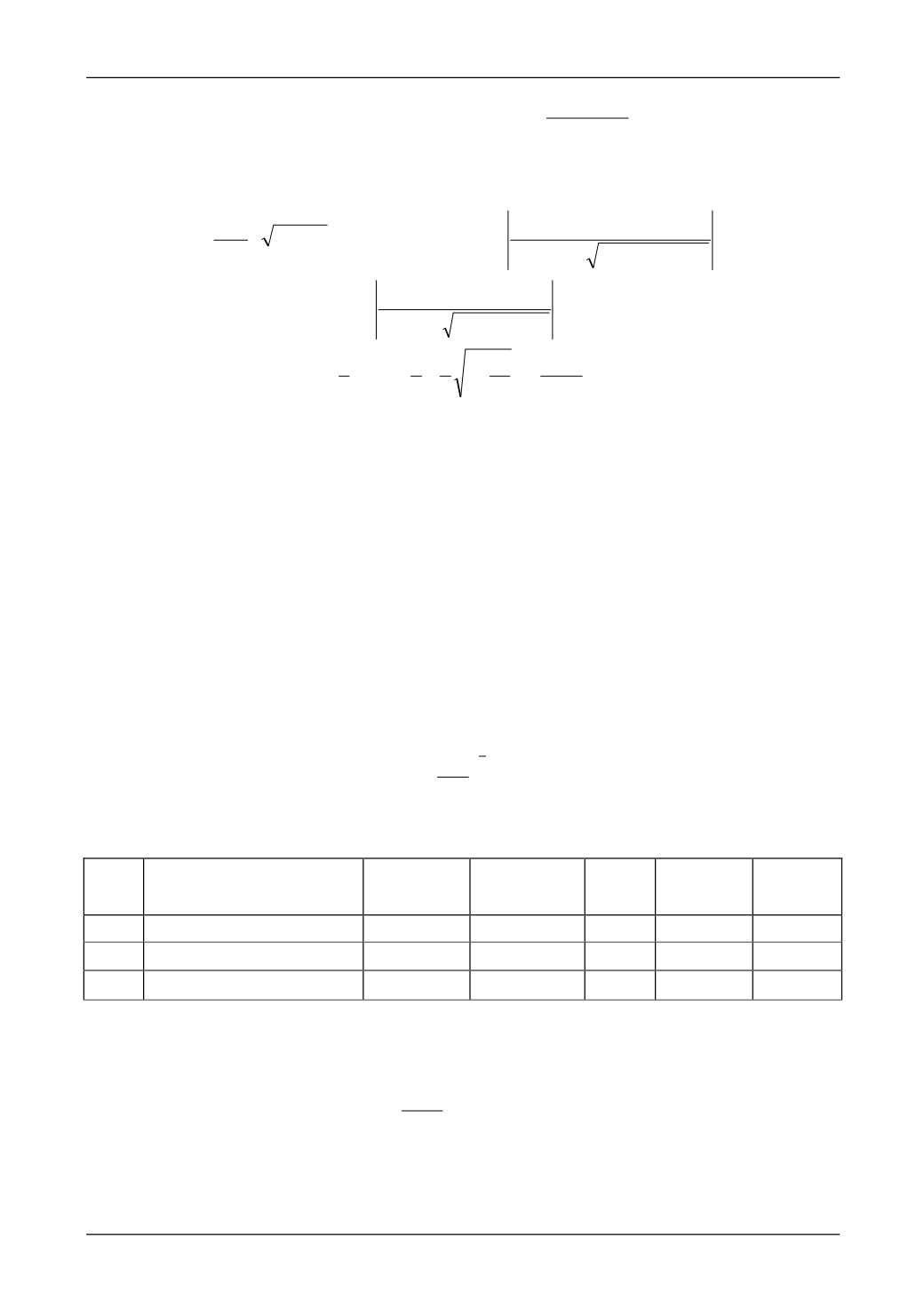
Сp R dX b Xqkk
(1)
Для модели реального газа учитываем результаты работы [17].
Для затворов с симметричными просветами сечений профилей золотника и седла распределе-
ние нормального контактного давления и ширина зоны контакта определяются согласно [13]:
2
2
n
B
-X
BX 1
XB
B X B
X
r
c
Xq
1 1
)ln
(
arccos
2
1
2
) (
2
;
1 1
1
ln
2
2
B -X
BX
XB
BX
(2)
.
2
1
arccos
2
2
c
q
c
b
c
b
c
b
r
c
ln
(3)
Выражения (1)-(3) с учетом того, что
1
1
dXXqc q
n
l
,
(4)
составляют замкнутую систему уравнений, позволяющую для каждого набора параметров
n
определить значение
l
q
, обеспечивающее заданную герметичность
l
Q
. После определения
l
q
сле-
дует произвести проверку следующего функционального ограничения – статической прочности. Учи-
тывая, что согласно исходным условиям закрытие (нагружение) затвора может происходить при от-
сутствии давления среды, проверку на статическую прочность следует производить при общей на-
грузке
N
.
Условие статической прочности
l
n
экв
q
,
,
(5)
где
экв
- максимальное эквивалентное напряжение, определяемое согласно [15, 16].
Проверка объемной усталостной прочности производится по выражению
,
1
N
N
n
o
экв
y
(6)
где
0
,
n
константы для данной марки материала (табл. 1)
Таблица 1
№
п/п
Марка
материала
o
экв
,
МПа
n
в
,
МПа
т
,
МПа
Е
,
ГПа
1
сталь30Х13
2820
0,0625
850
710
223
2
сталь38ХНМА
1830
0,0965
1080
930
213
3
сталь40ХН2МА
1755
0,058
1080
930
215
Следующим функциональным ограничением является условие долговечности. Число циклов
нагружений, при котором сохраняются требования по герметичности, определяется кривой фрикци-
онной усталости затвора, которая описывается уравнением [16]
,
0
0
max
N N q
c
m
n
(7)
где
4
10
o
N
базовое число циклов;
5,2...5,1
m
- параметр кривой выносливости, где меньшее
значение соответствует применению более высококачественных материалов без существенных дина-














