
Конструкции, технические и эксплуатационные свойства транспортных средств
315
cos
cos
sin
cos
1
4
1
i
l
l i
b
.
(7)
Увеличение расстояния
l
4
(или
l
3
) приводит к увеличению параметра
b
. Для составления урав-
нения движения системы, схема которой приведена на рис. 1,
в
, то, составим выражения для кинети-
ческой и потенциальной энергий:
2
2
1
2
1
2
1 T
B
ym yM
,
(8)
2
2
1 П
z yk
.
(8′)
Уравнение движения системы примет вид
Q ky
mb My
2
1
.
(9)
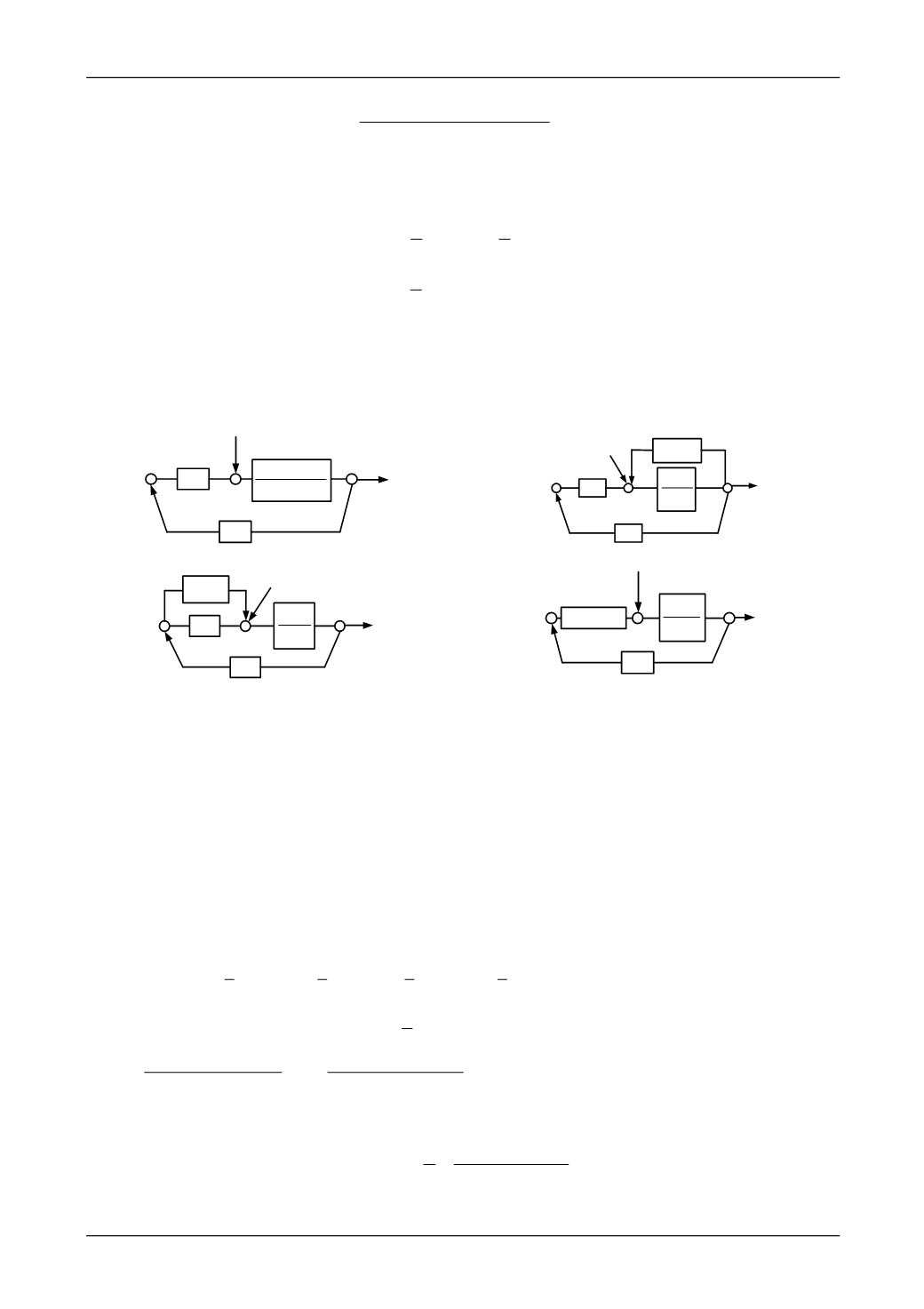
На основании (9) получены структурные схемы системы (рис. 2,
а
–
г
).
а
)
Q
~
y
~
k
2 2
1
1
p mb M
1
б
)
Q
~
y
~
k
2
1
Mp
1
2 2
1
pmb
в
)
Q
~
y
~
k
2
1
Mp
1
2 2
1
pmb
г
)
Q
~
y
~
2 2
1
pmb k
2
1
Mp
1
Рис. 2. Структурные схемы виброзащитных систем:
а
– система обладает приведенной массой
2
1
mb M
;
б
– УПД является обратной дополнительной связью по
ускорению по отношению к объекту защиты;
в
– УПД как параллельное звено;
г
– упругий элемент и УПД могут соединяться по правилам параллельного соединения пружин
(«~» – изображение переменных по Лапласу [10])
Таким образом, УПД при силовом возмущении трансформируется в звено с передаточной
функцией типового дифференцирующего элемента второго порядка. Способы введения такой допол-
нительной связи соответствуют правилам преобразований в структурной теории виброзащитных сис-
тем. Введение УПД может рассматриваться как способ управления частотой собственных колебаний.
Для этих целей могут варьироваться параметры рычагов, дополнительной массы
m
и углы установки
звеньев.
Особенности динамических свойств системы при кинематических возмущениях.
Выра-
жения для кинетической и потенциальной энергий системы при кинематическом возмущении
yzbaa
z a y am z yM y m z yM
B
21
2
1
2
2
2
2
2
2
1
2
1
2
1
2
1 T
(10);
2
2
1П
z y k
,
(11)
где
cos
cos
sin
cos
i
i
a
;
cos
cos
sin
cos
1
i
a
;
b
2
= cosα·cosβ – sinα·sinβ.
Используя уравнение Лагранжа второго рода и преобразования Лапласа, получим выражения
для передаточной функции при входном воздействии
z
~
и выходном –
y
~
k pmaM
k mp baa
z
y pW
2
2
2
21
~
~
,
(12)














