
Механики XXI веку. №15 2016 г.
136
плоскостей Σ и Δ проецируется в точку
G
. Введем точки
1
L
и
2
L
, располагающиеся на картинной
плоскости и лежащие на прямой
g
, которая проходит через точку
M
и перпендикулярна прямой
e
,
по которой пересекаются картинная и предметная плоскость [12]. Точки
1
L
и
2
L
располагаются на
одинаковом расстоянии от точки
M
по разные стороны от нее. Расстояние
2
1
LM LM
обозна-
чим через
s
. Прямая
g
, на которой лежат соответствующие точки
1
L
и
2
L
, так же перпендикулярна
прямой
e
, как и прямая
g
[13]; координаты точек
1
L
и
2
L
могут быть найдены по той же методике,
что и координаты точки
M
выше.
Из рисунка 3 видно, что точка
H
, принадлежащая прямой g, представляет из себя прообраз
бесконечно удаленной точки
H
прямой
g
. Отсюда следует вывод, что на прямой
g
имеется гар-
моническая четверка точек:
2 1
, ,
,
LLHM
. Из условий проецирования следует, что и на прямой
g
имеется гармоническая четверка точек:
2 1
, , ,
LLHM
[14, 15], т. е. сложное отношение указанных то-
чек
1
) , , , (
2
1
2
1
2 1
LMLH
LHLM
LLHM
. С учетом того, что
1 2
2
1
LL LH LH
(в соответствии с ри-
сунком 3), расстояние от точки
H
до точки
M
можно найти с помощью формулы:
ML LHMH
2
2
,
(2)
где
2
1
2
1 2
2
LMLM
LMLL
LH
.
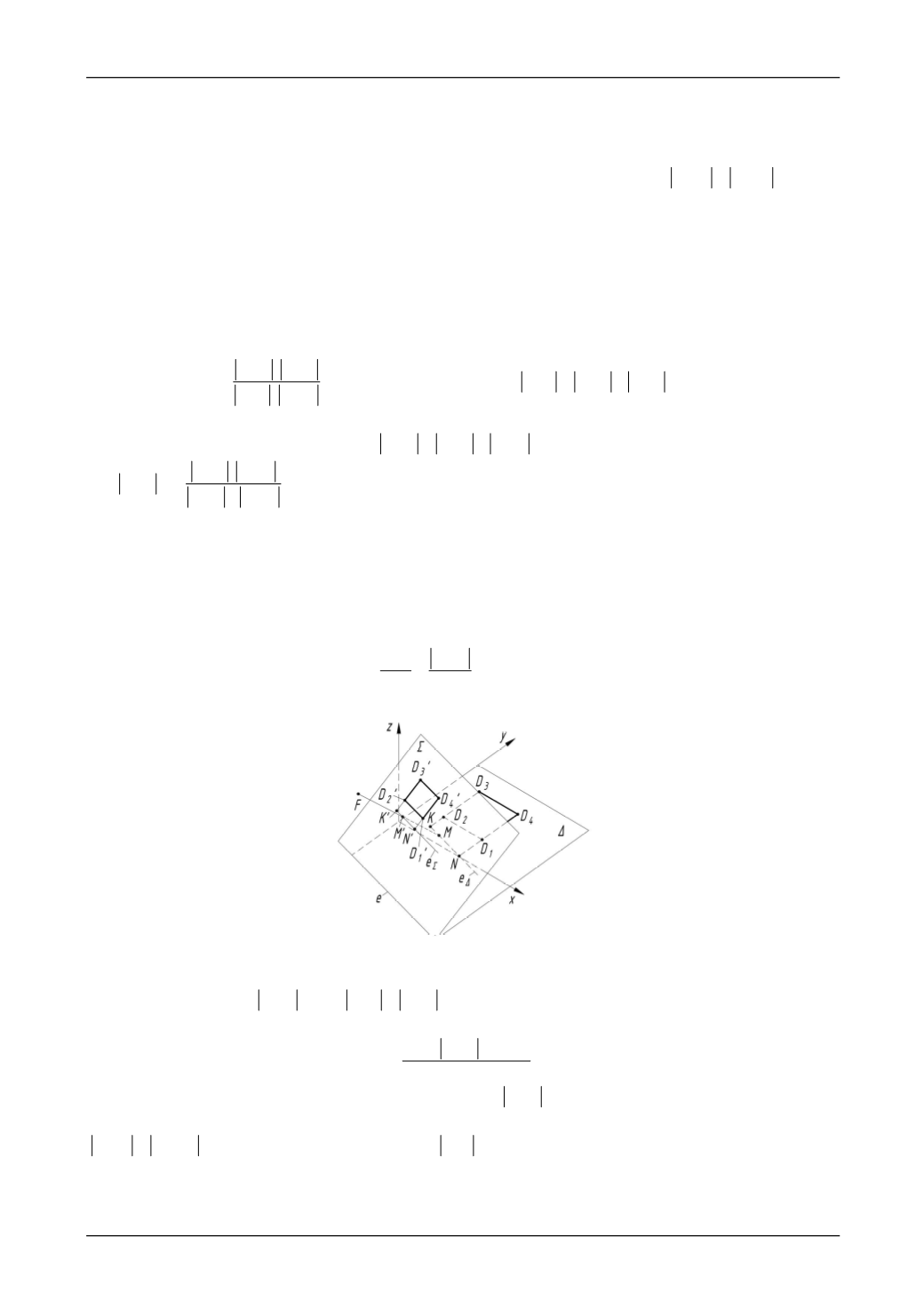
Чтобы найти выражение для определения расстояния
t
между оптическим центром и картин-
ной плоскостью, в предметной плоскости проводится прямая
e
, проходящая через точку
M
парал-
лельно прямой e (в соответствии с рисунком 4) [14]. Данная прямая будет пересекать продолжения
сторон квадрата в двух точках
K
и
N
, расстояние между которыми обозначим через
k
, а расстоя-
ние между точками
K
и
N
, принадлежащими соответственной прямой
e e
||
в картинной плоско-
сти – через
k
. Из подобия треугольников
FKN
и
NKF
следует отношение:
MF
MF
k
nk
.
(3)
Рис. 4. Определение расстояния
t
Учитывая, что
t
MF
и
)
cos(
k
MHMF
(в соответствии с рисунком 3), выражение (4)
можно разрешить относительно
t
:
k
k
MHnk
t
)
cos(
.
(4)
В выражении (5) неизвестны
n
и
k
; расстояние
MH
было определено выше.
Чтобы определить угол тангажа
k
, вернемся к рисунку Рис. 3, где расстояние
s LM LM
2
1
. Найдя по теореме синусов
VL
2
из треугольника
VLL
2 1
, выразив угол
из от-
ношения пропорциональных сторон подобных треугольников
VLF
2
и
1 2
LLF
, подставив в получен-














