
Современные технологии и автоматизация в машиностроении
135
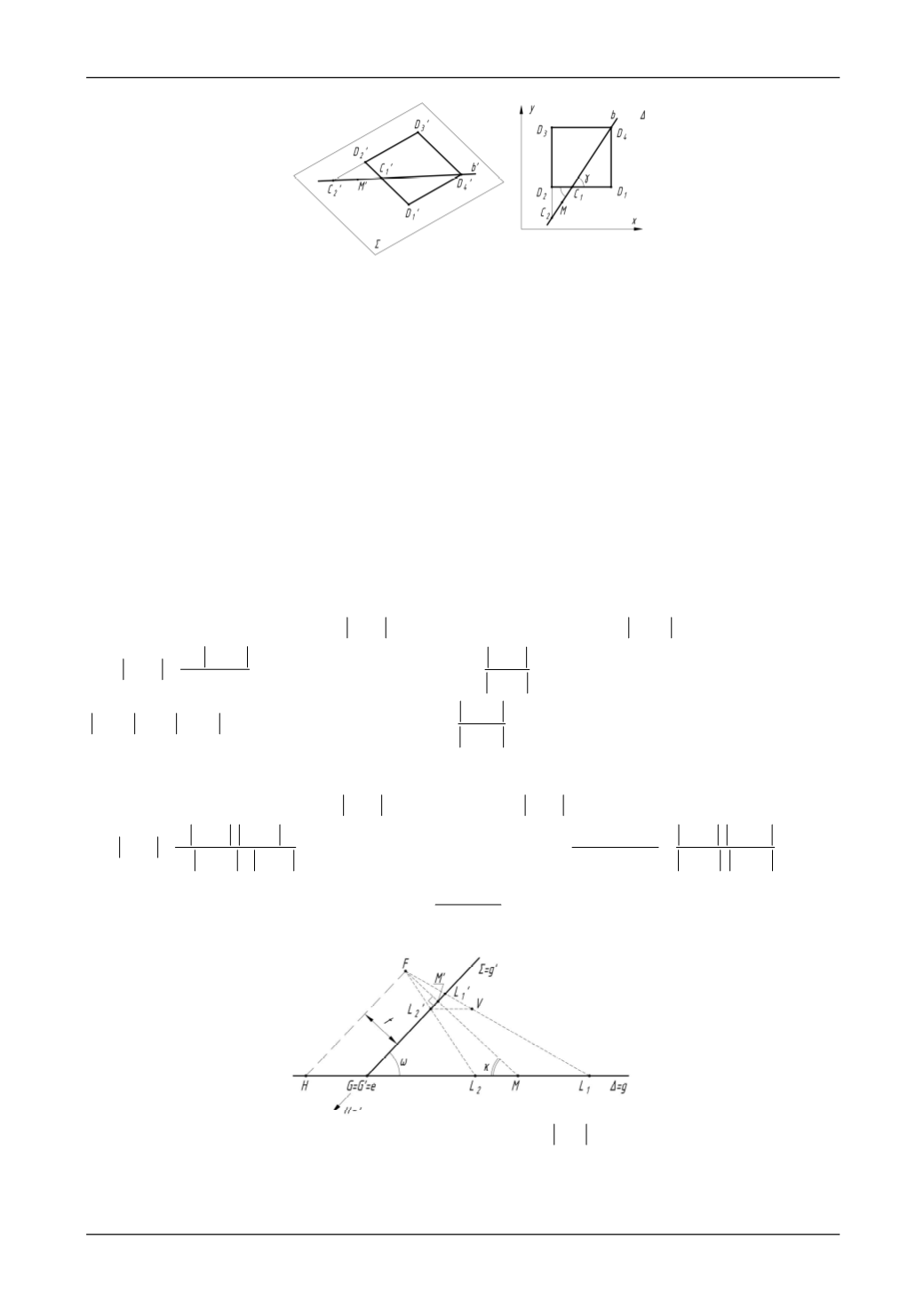
Рис 2. Определение вспомогательных точек
1
C
и
2
C
в плоскости
и соответствующих им точек
1
C
и
2
C
в плоскости
С целью нахождения
t
и
n
будем использовать квадрат с заведомо известным положением в
предметной системе координат. Координаты вершин изображения данного квадрата система в со-
стоянии вычислить автоматически [11].
Пусть прямая
b
– прямая, проходящая через точку
M
и одну из вершин квадрата, например,
вершину
4
D
(в соответствии с рисунком 2). Соответственную ей прямую в плоскости
назовем
b
.
Отталкиваясь от условий проецирования, можно утверждать, что точкам
4 3 2 1
,
,
,
DDDD
, ин-
цидентным плоскости
, соответствуют точки
,
,
,
,
4 3 2 1
DDDD
инцидентные плоскости
. В плоско-
сти Σ введем точку
1
C
, получаемую на пересечении прямой
b
со стороной квадрата
2 1
DD
(т. е.
2 1
4
1
DD DM C
), а также точку
2
C
, получаемую на пересечении прямой
b
с продолжением
стороны квадрата
3 2
DD
(т.е.
3 2
4
2
DD DM C
).
Координаты соответствующих точек
1
C
и
2
C
в плоскости
могут быть найдены по форму-
лам:
2 2
1 1
2
2
2
2
1
1
1
1
;
;
;
CD y y x x y y CD x x
D C D C D C
D C
,
(1)
где
1
2 1 1
1 1
1
z
DDz
CD
;
1 2
1 1
1 2 1
1 2 1
1
,
,
,
,
CD
CD
CDD CDD z
– простое отношение точек
1 2 1
, ,
CDD
;
2 3 2
2 2
DD z CD
;
2 3
2 2
2 3 1
2 3 2
2
, ,
, ,
DD
CD
DDC DDC z
.
Далее находятся координаты точки
M
пересечения оптической оси камеры с предметной
плоскостью:
)
sin(
);
cos(
1
1
1
1
CM y y
CM x x
C M
C M
,
(1)
где
;
1 2
2 4
4 1 1 2
1
CC CD
DCCC
CM
2 4 1
4
1 2
4
2
1
2
4 1
2
4 1
2
,
,
,
,
, , ,
, ,
,
CDCM
DMCC
DMC
CMC DCMC DCMC
– слож-
ное отношение точек
4 1
2
, ,
,
DCMC
;
1
4
1
4
C D
C D
x x
y y
arctg
(в соответствии с рисунком 2).
Рис. 3. Определение расстояния
HM
На следующем этапе определяется расстояние от точки
M
до точки
H
(в соответствии с ри-
сунком 3). На рисунке 3 плоскости Σ и Δ занимают проецирующее положение, линия e пересечения














